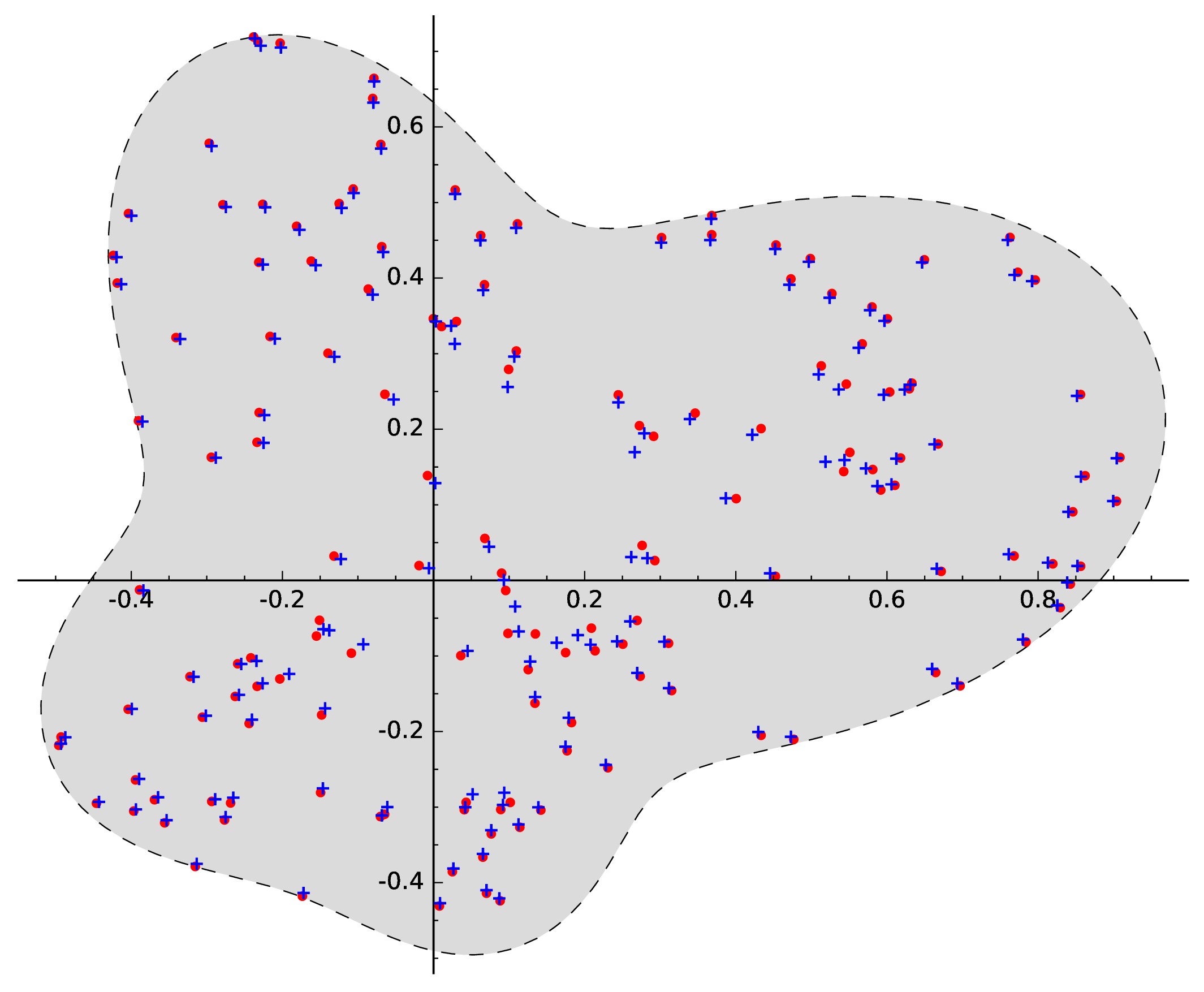
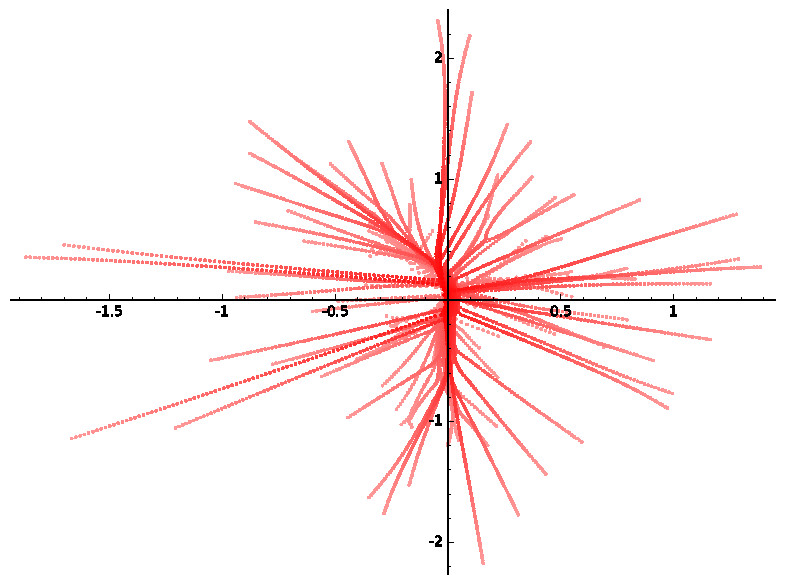
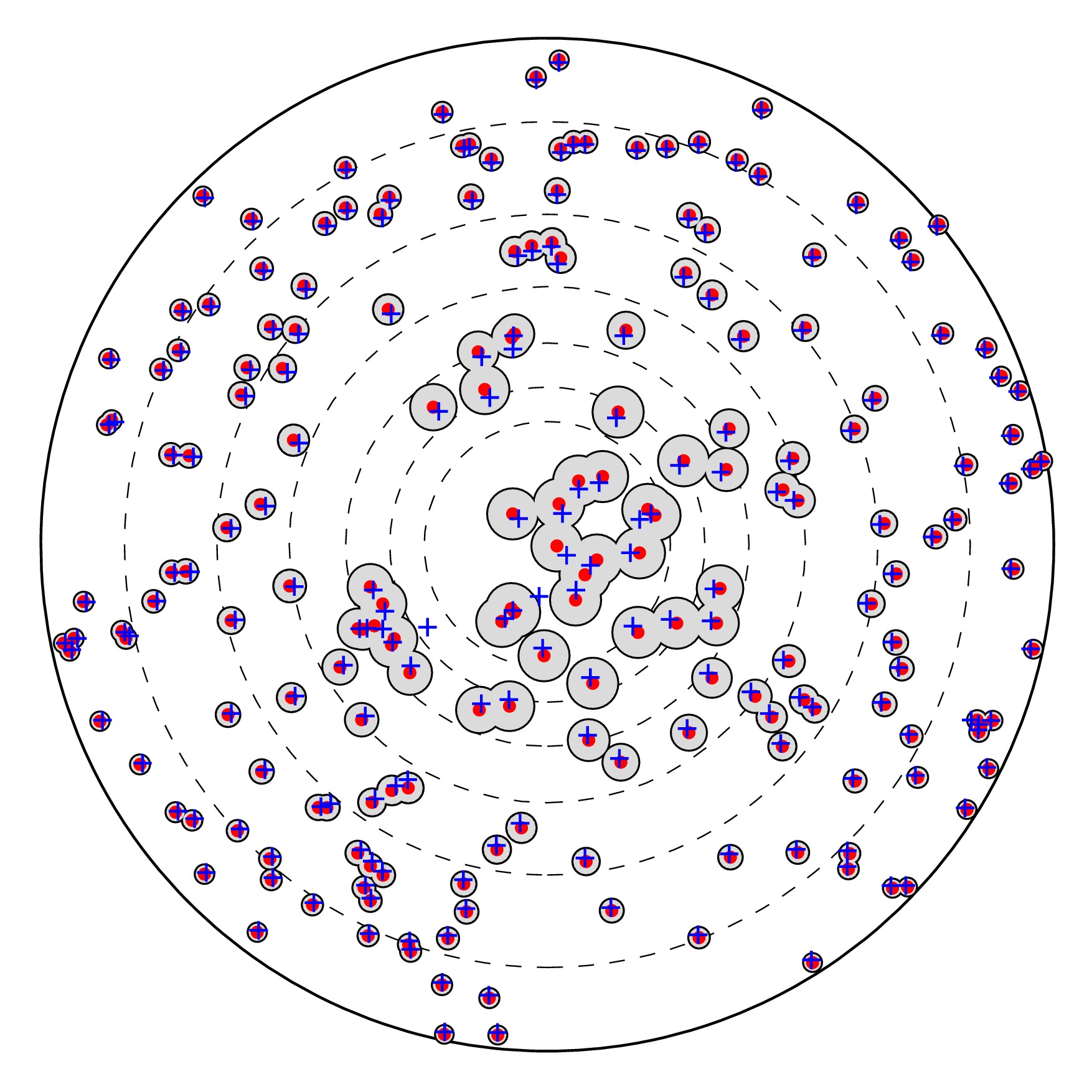
I study probability theory and its applications to random polynomials and random matrices. My recent work with Sean O'Rourke (University of Colorado Boulder) concerns pairing between the roots and critical points of random polynomials.
Publications:
- S. O'Rourke, N. Williams, An asymptotic refinement of the Gauss–Lucas theorem for random polynomials with i.i.d. roots. Under review. Available at
https://arxiv.org/abs/2409.09538.
- T. Greenwood, J. Kariv, N. Williams, From discrete to continuous: Monochromatic 3-term arithmetic progressions. Math. Comp. 93 (2024) No. 350, 2959–2983. Electronically published on May 16, 2024, DOI:
https://doi.org/10.1090/mcom/3970.
- S. O'Rourke, N. Williams, Partial linear eigenvalue statistics for non-hermitian random matrices. Theory Probab. Appl. 67 (2023) No. 4, 613–632. Available at
https://doi.org/10.1137/S0040585X97T991179 and https://doi.org/10.4213/tvp5462.
- S. O'Rourke, N. Williams, On the local pairing behavior of critical points and roots of random polynomials. Electron. J. Probab. 25 (2020), 1–68. Available at
https://projecteuclid.org/euclid.ejp/1597737717.
- A. Brisbin, M. Riehl, N. Williams, The Deletion-Insertion Model Applied to the Genome Rearrangement Problem. Pure Math. Appl. (PU.M.A.) 28 (2019), No. 1, 1–13. Available at
https://doi.org/10.1515/puma-2015-0030.
- S. O'Rourke, N. Williams, Pairing between zeros and critical points of random polynomials with independent roots. Trans. Amer. Math. Soc. 371 (2019), No. 4, 2343–2381. Available at
https://doi.org/10.1090/tran/7496.
- Christy, J., McHugh, J., Riehl, M. and Williams, N. Distribution of genome rearrangement distance under double cut and join. Involve 7 (2014), No. 4, 491–507. Available at
https://doi.org/10.2140/involve.2014.7.491.
- Christy, J., McHugh, J., Riehl M., and Williams, N. Maximally distant genomes under the DCJ operation. Abstract published in the proceedings of the Permutation Patterns Conference, 2010, Dartmouth New Hampshire.